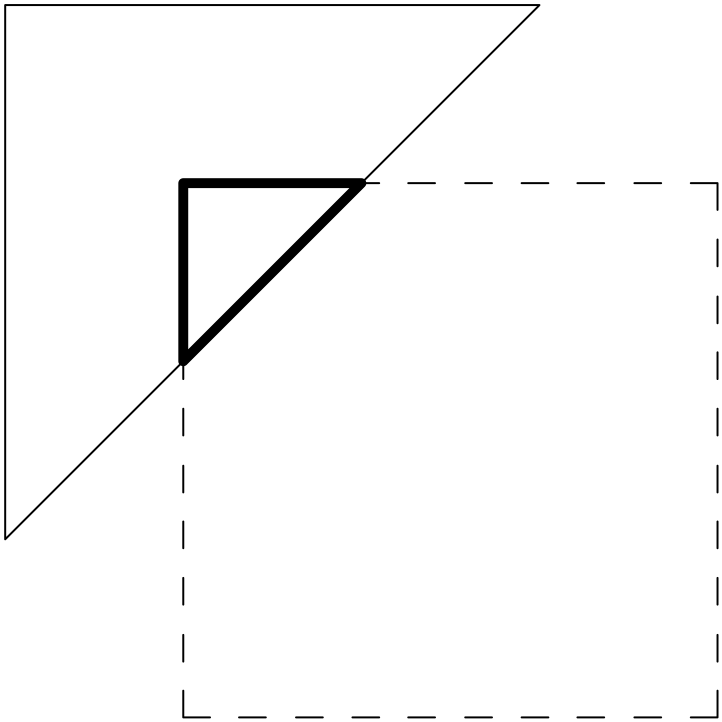
It is often necessary, particularly in graphics applications, to “clip” a given polygon with another. The figure below shows an example where we would like to clip the solid triangle with the dashed rectangle to obtain the bold triangle. In this article, we'll look at the particular case where the clipping polygon is a rectangle which is oriented parallel with the axes. For this case, the Sutherland-Hodgeman algorithm is often employed. This is the algorithm we will explore.

The Sutherland-Hodgeman polygon clipping algorithm is relatively straightforward and is easily implemented in C. It does have some limitations, which we'll explore later. First, let's see how it works.
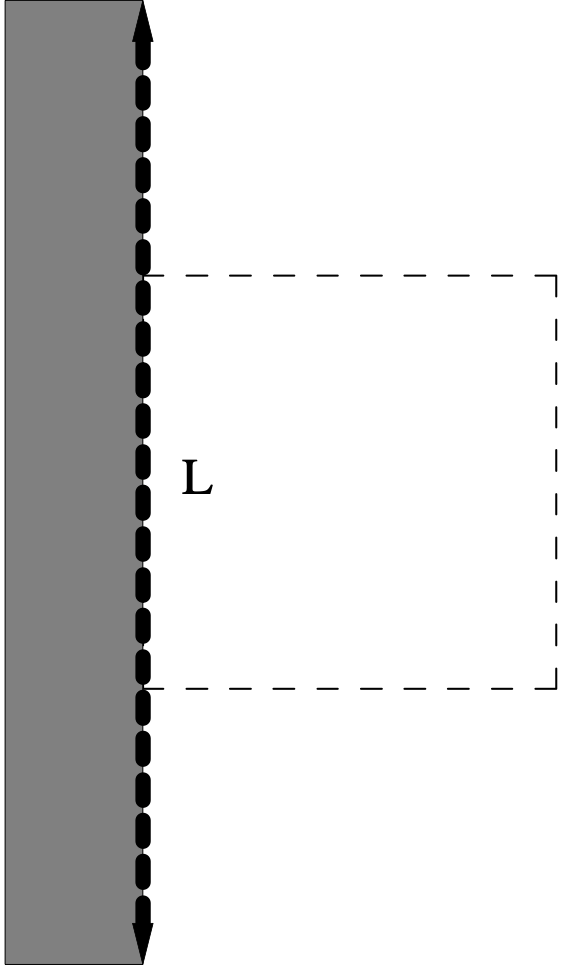
For each of the four sides of the clipping rectangle, consider the line L through the two points which define that side. For each side, this line creates two planes, one which includes the clipping rectangle and one which does not. We'll call the one which does not include the clipping rectangle the “clipping plane” (shown shaded in the figure below.)
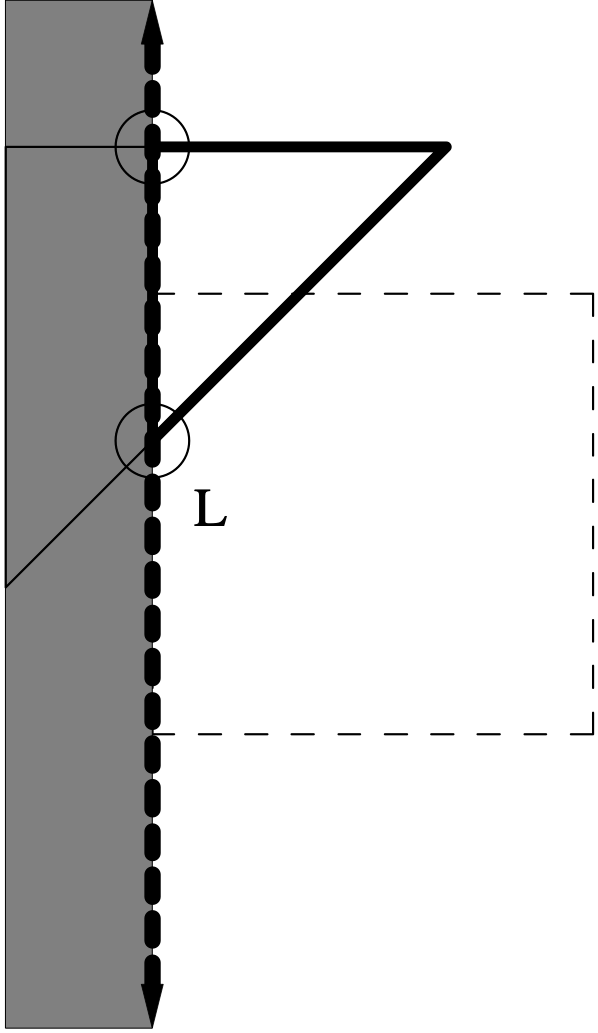
For each of the four clipping planes, we must remove any vertices of the clipped polygon which lie inside the plane and create new points (circled in the figure below) where the segments associated with these vertices cross the line L.
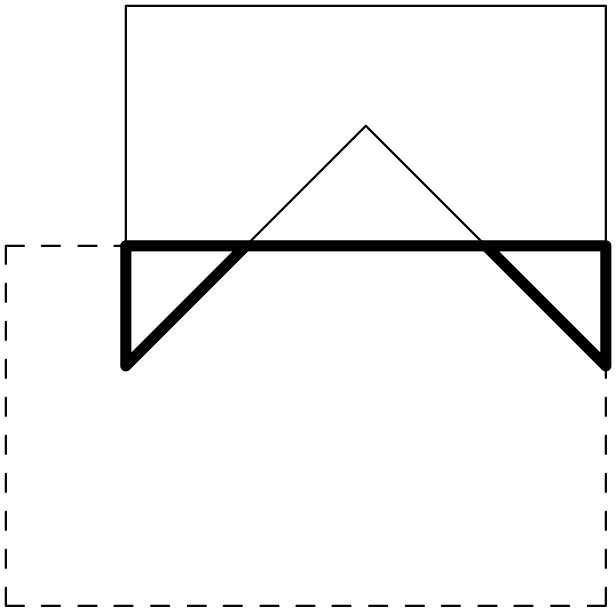
After clipping each of the four planes, we are left with the clipped polygon.
This algorithm always produces a single output polygon, even if the clipped polygon is concave and arranged in such a way that multiple output polygons might reasonably be expected. Instead, the polygons will be linked with overlapping segments along the edge of the clipping rectangle. This may or may not be the desired result, depending on your application.
We'll now implement this algorithm in C. The code presented is structured to
illustrate the algorithm as discussed. I haven't taken any measures to verify
its correctness or to optimize it for performance or memory usage. It's mostly
common C, but I did use some C99 macros (compile with --std=c99 if
you use gcc).
First, we'll be using some things from math.h and assert.h.
#include <math.h> #include <assert.h>
Next, we have some #defines and structs to make the remainder of the code more readable.
#define CP_MAXVERT 32
#define CP_LEFT 0
#define CP_RIGHT 1
#define CP_TOP 2
#define CP_BOTTOM 3
struct rect {
double t; /* Top */
double b; /* Bottom */
double l; /* Left */
double r; /* Right */
};
struct point {
double x;
double y;
};
To determine the correct course of action in the main algorithm, we'll need to be able to check if a given point is “inside” or “outside.” In this sense, we take “outside” to mean “within the clipping plane.” This function takes the point in question, the clipping rectangle, and a number indicating which side of the rectangle is forming the clipping plane.
int cp_inside (struct point p, struct rect r, int side) {
switch (side) {
case CP_LEFT:
return p.x >= r.l;
case CP_RIGHT:
return p.x <= r.l;
case CP_TOP:
return p.y <= r.t;
case CP_BOTTOM:
return p.y >= r.b;
}
}
When one of the two points defining a line segment is “inside” and the other is “outside,” we will need to create a new vertex where the segment intersects the clipping rectangle. This function takes the “inside” point (p), the “outside” point (q), the clipping rectangle, and again the side in question. It first finds the slope (a) and y-intercept (b) of the line segment pq. Now, depending on the side under consideration, either the x or y component of the new point is set equal to that of the bounding side and the remaining component is computed using the slope and intercept previously found. When considering the top or bottom sides, it is possible that the segment pq is vertical. This condition can be recognized when the slope (a) is infinite. In this special case, the x component of the new point will be the same as the x component of p or q.
struct point cp_intersect (struct point p, struct point q, struct rect r,
int side) {
struct point t;
double a, b;
/* Find slope and intercept of segment pq */
a = (q.y - p.y) / (q.x - p.x);
b = p.y - p.x * a;
switch (side) {
case CP_LEFT:
t.x = r.l;
t.y = t.x * a + b;
break;
case CP_RIGHT:
t.x = r.r;
t.y = t.x * a + b;
break;
case CP_TOP:
t.y = r.t;
t.x = isfinite(a) ? (t.y - b) / a : p.x;
break;
case CP_BOTTOM:
t.y = r.b;
t.x = isfinite(a) ? (t.y - b) / a : p.x;
break;
}
return t;
}
Finally, we can dive into the real meat of the algorithm. This function clips the clipped polygon against the clipping plane for a particular side of the clipping rectangle. Starting with the first vertex in the clipped polygon, we consider each vertex (p) along with the one before it (s). There are four ways that these two points may be arranged:
void cp_clipplane (int *v, struct point in[CP_MAXVERT], struct rect r,
int side) {
int i, j=0;
struct point s, p;
struct point out[CP_MAXVERT];
s = in[*v - 1];
for (i = 0; i < *v; i++) {
p = in[i];
if (cp_inside(p, r, side)) {
/* Point p is "inside" */
if (!cp_inside(s, r, side)) {
/* p is "inside" and s is "outside" */
out[j] = cp_intersect(p, s, r, side);
j++;
}
out[j] = p;
j++;
} else if (cp_inside(s, r, side)) {
/* s is "inside" and p is "outside" */
out[j] = cp_intersect(s, p, r, side);
j++
}
s = p;
}
/* Set return values */
for (i=0; i < *v; i++) {
in[i] = out[i];
}
}
The actual clippoly function is very simple: it calls the previous function (cp_clipplane) once for each side of the clipping rectangle. First, though, it performs a few tests to make sure that the input data make sense and that there will be room to store the output polygon.
void clippoly (int *v, struct point p[CP_MAXVERT], struct rect r) {
assert(*v <= CP_MAXVERT / 2);
assert(r.l < r.r);
assert(r.b < r.t);
cp_clipplane(v, p, r, CP_LEFT);
cp_clipplane(v, p, r, CP_RIGHT);
cp_clipplane(v, p, r, CP_TOP);
cp_clipplane(v, p, r, CP_BOTTOM);
}
We've seen that the Sutherland-Hodgeman polygon clipping algorithm is a straightforward algorithm for clipping a given polygon with a rectangle and that it can be easily implemented in C.
I hope that you've found this article interesting and helpful. If this is the kind of thing you're into, you may enjoy my other articles. If you have any comments or questions, please drop me a line at the address below.
Aaron D. Parks